En el apasionante mundo del diseño y la geometría, el término «convexo» despierta la curiosidad de muchos. En este artículo, exploraremos a fondo la definición y el concepto de «convexo», y cómo este concepto se relaciona con diversas disciplinas, desde la matemática hasta el diseño industrial. Acompáñanos en este viaje informativo y educativo para comprender a profundidad el mundo de lo convexo.
¿Qué es Convexo?
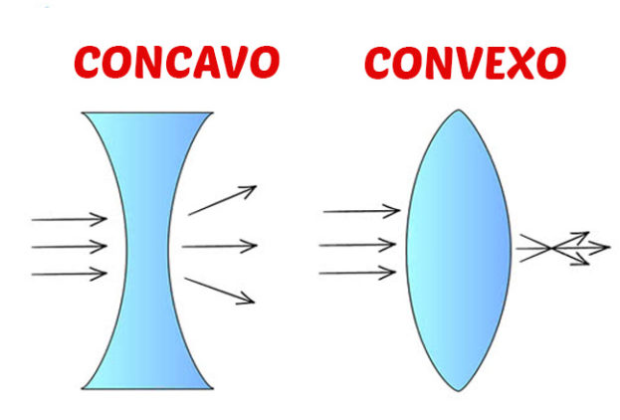
Convexo es un adjetivo que se utiliza para describir una forma o figura que se curva hacia afuera o se hincha en lugar de hundirse o ceder hacia adentro. En otras palabras, un objeto convexo se caracteriza por tener una superficie que se aleja gradualmente del centro o el punto más profundo. Esta característica es esencial para distinguirlo de su opuesto, que es cóncavo, donde la superficie se curva hacia adentro.
Ejemplos de Objetos Convexos
Para comprender mejor el concepto de convexo, es útil observar ejemplos concretos:
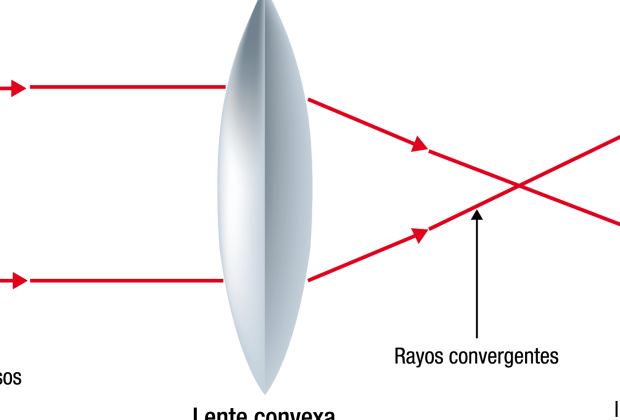
- Lentes Convexas: Uno de los ejemplos más comunes de objetos convexos son las lentes convergentes utilizadas en gafas y dispositivos ópticos. Estas lentes tienen una forma curvada hacia afuera y ayudan a enfocar la luz en un punto específico.
- Espejos Convexos: Los espejos convexos son ampliamente utilizados en la seguridad vial, ya que proporcionan una vista panorámica y ampliada de las carreteras. Su superficie curvada hacia afuera permite reflejar una mayor área.
- Cúpulas: Las cúpulas arquitectónicas suelen tener una forma convexa, lo que les permite distribuir uniformemente la carga y proporcionar una apariencia majestuosa.
- Frutas y Verduras: Muchas frutas y verduras, como manzanas, naranjas y tomates, tienen una forma convexa en su parte exterior, lo que les da su aspecto característico.
Importancia en Matemáticas
En el campo de las matemáticas, el concepto de convexidad juega un papel crucial. La teoría de conjuntos convexos es fundamental en áreas como la optimización, la geometría y la programación lineal. Un conjunto convexo es aquel en el que, dados dos puntos cualesquiera dentro del conjunto, la línea que los conecta también está completamente contenida dentro del conjunto.
La convexidad se utiliza para resolver una amplia gama de problemas en matemáticas aplicadas y teoría de optimización. Desde encontrar la ruta más corta entre dos puntos en un grafo hasta determinar la mejor asignación de recursos, la convexidad es una herramienta invaluable en la resolución de problemas.
Diseño Industrial y Convexidad
En el mundo del diseño industrial, la convexidad desempeña un papel esencial en la creación de productos ergonómicos y atractivos visualmente. Los diseñadores utilizan superficies convexas para mejorar la comodidad de los productos y su estética.
Un ejemplo clásico de diseño convexo es el elegante y ergonómico diseño de las sillas modernas. La curva hacia afuera de la superficie del asiento se adapta de manera natural a la forma del cuerpo humano, brindando comodidad y apoyo.
Usos de la Convexidad en la Ciencia de Datos
La convexidad también juega un papel crucial en la ciencia de datos y el análisis de algoritmos. En el ámbito de la optimización, los problemas convexos son especialmente relevantes. Un problema de optimización convexa se caracteriza por tener una función objetivo convexa y un conjunto de restricciones también convexas.
La importancia de los problemas convexos en la ciencia de datos radica en la solución eficiente que ofrecen. A diferencia de los problemas no convexos, los problemas convexos tienen soluciones únicas y globales. Esto significa que, dado un problema convexo, existe una solución que es la mejor posible en términos de optimización, y esta solución es alcanzable de manera eficiente mediante algoritmos específicos.
Un ejemplo destacado de la aplicación de la convexidad en la ciencia de datos es la regresión lineal, que es un método utilizado para ajustar una línea recta a un conjunto de datos. La función objetivo en la regresión lineal es convexa, lo que garantiza que el algoritmo converja a la mejor solución.
Arte y Estética: Convexidad en la Escultura
La convexidad también ha desempeñado un papel importante en el mundo del arte y la escultura. Muchos escultores han utilizado la forma convexa en sus obras para lograr efectos visuales únicos y atractivos.
Un ejemplo icónico de esto es el «David» de Miguel Ángel, una de las esculturas más famosas del Renacimiento. El cuerpo de David está modelado con curvas suaves y superficies convexas que capturan la belleza y la perfección del cuerpo humano. La elección de utilizar la convexidad en esta obra maestra no solo resalta la habilidad técnica del escultor, sino que también contribuye a la sensación de belleza y armonía que emana de la escultura.
Otro ejemplo es la escultura moderna, donde artistas contemporáneos han experimentado con superficies convexas para crear obras de arte abstractas y vanguardistas. La convexidad se convierte en una herramienta expresiva que permite a los artistas jugar con la luz y la sombra, creando efectos visuales fascinantes.
En Resumen
En resumen, la convexidad es un concepto fundamental que se encuentra en diversas disciplinas, desde las matemáticas hasta el diseño industrial. Se refiere a la característica de una superficie que se curva hacia afuera en lugar de hacia adentro. Los objetos convexos son comunes en la vida cotidiana y desempeñan un papel crucial en la resolución de problemas matemáticos y el diseño de productos.